Метрики кластеризации

Кластеризация метрик - процесс группировки наблюдаемых данных на основе схожести между ними. В области машинного обучения это относится к задаче без учителя, где алгоритм выявляет скрытую структуру в данных без какого-либо предварительного обучения.

Метрика кластеризации может быть использована для следующих задач:

• выявление групп пользователей на основе их поведения на сайте;
• анализ групп товаров по продажам и другим характеристикам;
• оценка эффективности маркетинговых кампаний по различным каналам продвижения.

Объединение в кластеры помогает найти скрытые зависимости и структуры в данных, которые могут быть использованы для принятия важных бизнес-решений.

Кластеризация метрик - это процесс разделения данных на группы или кластеры на основе их сходства и различий. Особенности процесса включают в себя следующие моменты:

• подбор показателей - для кластеризации необходимо выбрать точку данных, которая измеряет различия между объектами. Это может быть евклидово расстояние, косинусная мера сходства, корреляция;
• выбор алгоритма - существует множество алгоритмов, которые используют различные методы для определения сходства и различий между объектами. Некоторые из них включают k-means, иерархическую кластеризацию, DBSCAN;
• подбор числа кластеров - перед процедурой следует определить, сколько кластеров необходимо создать. Это может быть произведено с помощью множества методов, таких как метод локтя, силуэтный график;
• оценка качества - после группировки необходимо оценить качество группировки. Это может быть выполнено с помощью показателей, таких как индекс Данна, индекс силуэта;
• интерпретация результатов - процесс группировки не всегда легко интерпретируем. Необходимо осуществлять анализ и визуализацию данных, чтобы понимать, какие группы сформировались, и какие свойства объектов в этих группах могут быть общими.

Геометрическая интерпретация задачи кластеризации заключается в том, чтобы представить множество данных в виде точек в n-мерном пространстве, где n - количество признаков или характеристик, по которым производится группировка. Каждая точка соответствует отдельному объекту или экземпляру данных.

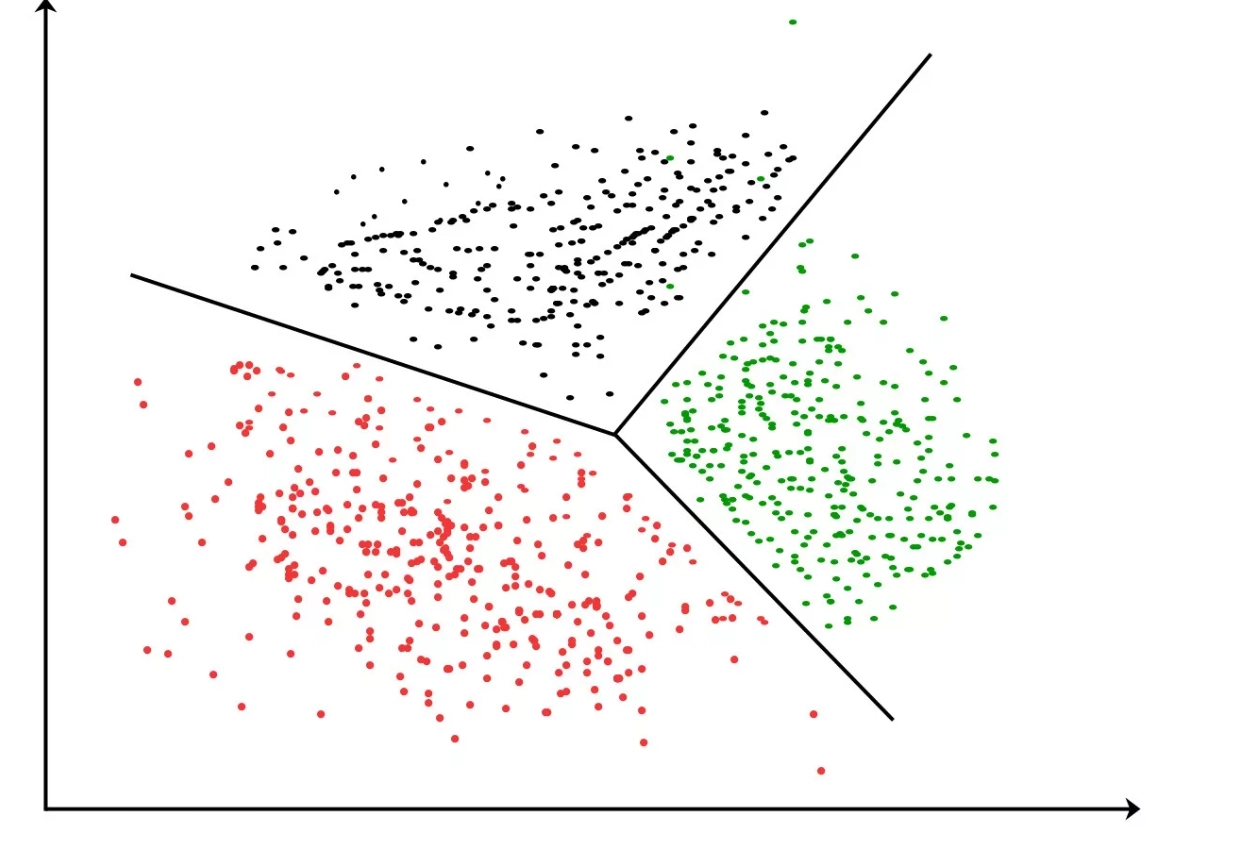
Такая задача в группировании данных в подмножества, называемые кластерами, заключается в том, чтобы объекты внутри каждого кластера были максимально похожи друг на друга, а объекты из разных кластеров были предельно различными. Геометрически это означает, что кластеры должны быть расположены близко друг к другу в пространстве, а между ними необходимо явное разделение.

Различные алгоритмы группировки используют разные подходы для выполнения этой задачи. Например, группирование k-средних использует итеративный алгоритм, который начинает с случайного выбора k точек в пространстве и затем находит ближайшие к ним точки до тех пор, пока не будет достигнуто определенное условие остановки.

Геометрическая интерпретация задачи объединения в кластеры позволяет наглядно представлять результаты группировки и проверять их на соответствие ожиданиям. Например, можно использовать визуализацию для выявления кластеров, которые сильно перекрываются, или для оценки эффективности различных алгоритмов на разных наборах данных.

Также перед процесом ставятся следующие задачи:

• идентификация необычных значений: кластерный анализ точки данных позволяет выявить необычные значения, которые могут сигнализировать о проблемах с производительностью или угрозах безопасности;
• группировка: процесс позволяет разбивать их в логические кластеры, что упрощает мониторинг и управление производительностью системы;
• выявление зависимостей: кластерный анализ показателей позволяет выявлять зависимости между различными группировками, что может помочь в поиске причин проблем с производительностью или безопасностью;
• улучшение производительности: процесс может помочь в оптимизации производительности системы путем выявления проблем;
• улучшение безопасности: разбиение показателей может помочь в обнаружении угроз безопасности и предотвращении их возникновения;
• прогнозирование будущего состояния системы: процесс может помочь в прогнозировании будущего состояния системы и идентификации возможных проблем заранее.

Количественные показатели имеют следующие свойства.

1. Положительность метрик: она исключает отрицательный результат.
2. Неравенство треугольника: должна следовать принципу, что путь от A до B должен быть не меньше, чем путь от A до C плюс путь от C до B.
3. Симметричность: для расстояния между A и B должна быть одинаковой при обратном порядке, т.е. расстояние между A и B должно быть таким же, как расстояние между B и A.
4. Однородность: сохранять свою форму при умножении на константу.
5. Различимость: должна отличать точки друг от друга, т.е. если расстояние между A и B равно 0, то это означает, что A и B находятся в одной точке.
6. Сходимость: должна быть полезной для определения предела последовательности точек.
7. Аддитивность: необходима для определения расстояния между точками, которые могут быть выражены в виде суммы более мелких расстояний.

Выделяют следующие разновидности.

1. Метрика посещаемости: количество посетителей, уникальных посетителей, просмотры страниц, среднее время на странице.
2. Метрики действий: количество кликов, конверсии, заполнение форм, заказы.
3. Метрики рекламы: CTR (кликабельность), CPC (стоимость за клик), CPA (стоимость за действие), ROAS (отношение дохода к затратам на рекламу).
4. Метрика социальных сетей: количество подписчиков, лайков, комментариев, ретвитов, охватов.
5. Метрика SEO: позиции в поисковых системах, трафик и CTR из поисковых систем, доля посещений по ключевым словам.
6. Метрика продаж: общая выручка, средний чек, количество заказов, возвратов.
7. Метрика удержания: клиентская лояльность, удержание клиентов, повторные покупки, отток клиентов.
8. Метрика производительности: время загрузки страниц, время ожидания ответа сервера, процент ошибок.

Анализ главных компонент (PCA) и кластерный анализ (CA) - это два различных метода статистического анализа данных, которые используются для обработки и суммирования информации о многомерных датасетах. Оба способа позволяют выделить наиболее значимые факторы или группы данных, упрощая их интерпретацию и облегчая последующий анализ.

PCA является методом преобразования исходных переменных в новые независимые переменные, называемые главными компонентами (PCs). Первый PC соответствует наибольшей части дисперсии, второй - следующей по величине, и т.д. Данные переменные могут быть использованы для уменьшения размерности исходного датасета, выделения основных трендов и упрощения дальнейшего анализа.

CA, с другой стороны, является методом объединения в кластеры данных на группы на основе сходства между наблюдениями. Сформированные кластеры могут быть использованы для выделения общих моделей поведения или характеристик, выявления аномалий или нетипичных элементов.

Одним из преимуществ PCA является возможность упрощения данных до нескольких главных компонент, что уменьшает количество переменных и повышает интерпретируемость результата. Однако, PCA может не учитывать важные различия между исходными переменными и скрытую двойственность в данных.

CA может лучше подходить для идентификации скрытых групп в данных, что полезно для поиска паттернов и описания сложных взаимодействий между переменными. Однако, CA требует настройки различных параметров и выбора определенных мер подобности, и может быть менее точным при обработке шума или сильно пересекающихся групп.

Вместе PCA и CA могут использоваться для получения более полного исследования данных, позволяя обнаружить скрытые корреляции между переменными и выделить их наиболее значимые группы.

Кластерный анализ - это метод многомерного статистического анализа, который используется для выделения групп схожих объектов или событий. Кластерный анализ может быть использован в различных областях, включая биологию, экономику, социологию, компьютерные науки.

Процесс кластерного анализа включает в себя группировку данных на основе их сходства или расстояния между ними. Например, если у нас есть данные о покупках клиентов в интернет-магазине, мы можем использовать кластерный анализ, чтобы выделить группы клиентов с похожими покупательскими поведениями.

Кластерный анализ имеет несколько типов, включая иерархический и неиерархический кластерный анализ. В иерархическом кластерном анализе мы строим дерево, которое показывает, как объекты группируются в кластеры. В неиерархическом мы определяем определенное количество кластеров и группируем объекты в соответствии с этим.

Анализ может быть полезен в выявлении очевидных и скрытых паттернов в данных, что может помочь в принятии более информированных решений. Однако, как и любой метод статистического анализа, кластерный анализ должен использоваться с осторожностью и оцениваться в контексте конкретной задачи или проблемы.

Методы кластеризации используются для группирования объектов в подмножества, которые имеют схожие свойства. Обзор методов можно разделить на следующие категории.

1. К-средних (k-means) - это метод кластеризации, который разбивает набор данных на заданное количество кластеров, так что объекты внутри каждого кластера находятся вблизи друг друга по определенной группировке.
2. DBSCAN - это метод, который основан на понятии плотности точек. Он находит области высокой плотности точек и определяет их как кластеры, а затем расширяет эти кластеры, добавляя точки, которые находятся вблизи границ кластеров.
3. Agglomerative clustering - это метод иерархической кластеризации, который начинает с каждой отдельной точки в качестве своего собственного кластера, а затем объединяет близлежащие кластеры на каждой итерации, пока не будет достигнуто заданное количество кластеров.
4. Gaussian mixture model - это метод, который моделирует каждый кластер как смесь гауссианских распределений. Предполагает, что каждый кластер имеет нормальное распределение точек, и пытается определить коэффициенты смеси и параметры каждого распределения, чтобы максимизировать вероятность наблюдаемых данных.

Модельные методы кластеризации используют вероятностную модель для описания распределений входных данных и построения кластеров. Нелинейные методы кластеризации (например, методы главных компонент) используются для преобразования исходных данных в более низких размерностях, которые могут быть более удобны для кластеризации.

Обзор методов кластеризации зависит от сложности анализируемых данных и необходимости поддержания высокой производительности алгоритма.

K-средние

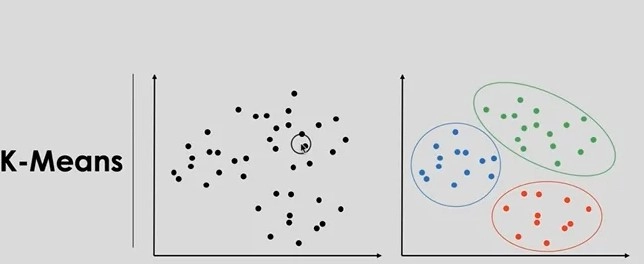
K-средние (англ. k-means) — это один из наиболее популярных алгоритмов кластеризации. Он относится к методам, основанным на расстояниях между точками в пространстве признаков. Алгоритм делит объекты на заранее неизвестное количество кластеров (центры кластеров выбираются случайно или иным способом). Расстояние между точками и центрами кластеров вычисляется на каждой итерации, после чего объекты перераспределяются по кластерам таким образом, чтобы минимизировать сумму квадратов расстояний между каждой точкой и центром кластера. Алгоритм повторяется до тех пор, пока центры кластеров не стабилизируются и не перестанут меняться. K-средние используются для решения задач различных областей, включая маркетинг, биоинформатику, генетику, космологию и другие.

 Низкоуровневый параллелизм

Алгоритм к-средних можно параллелить на несколько уровней. Низкоуровневый включает параллельное выполнение обработки данных на уровне инструкций процессора или параллельные вычисления на графическом процессоре. На уровне инструкций процессора может быть использован векторный параллелизм или параллельное выполнение инструкций без зависимостей. Векторный параллелизм применяют для одновременного выполнения операций на нескольких элементах данных. Например, если каждая точка в пространстве задана тремя координатами (x, y, z), то векторизованный код может обрабатывать несколько точек одновременно, что приводит к ускорению выполнения.

На графическом процессоре может быть использована параллельная обработка большого количества данных с помощью графических ядер. В этом случае каждое ядро может обрабатывать свою часть данных, что приводит к значительному ускорению выполнения алгоритма.

Можно использовать параллельную обработку данных на нескольких процессорах или вычислительных узлах. В этом случае каждый процессор может обрабатывать свою часть данных, что позволяет ускорить выполнение алгоритма, если данные достаточно большие для распределения их между процессорами.

Мини-партия K-средних

Это метод кластерного анализа, который применяется для разбиения набора данных на K кластеры. Каждый кластер представляет собой группу объектов, которые имеют похожие характеристики.

Процесс формирования кластеров в методе K-средних начинается с выбора K случайных центров кластеров. Затем каждый объект в наборе данных относится к ближайшему центру кластера. После этого они пересчитываются, основываясь на новообразованных кластерах, и процесс повторяется до тех пор, пока не достигнется стабильность в распределении объектов.

Мини-партия K-средних отличается от стандартного метода тем, что она обрабатывает данные более эффективно в случае больших объемов. Вместо того, чтобы обновлять центры кластеров после каждой итерации, мини-партия K-средних разбивает данные на более мелкие «пакеты» или мини-партии, и центры кластеров обновляются после обработки каждой из них. Это позволяет сократить количество итераций и уменьшить время работы алгоритма.

Распространение близости (Affinity Propagation) – это метод кластеризации, который использует подход попарного сравнения объектов и вычисления их схожести. Он определяет число кластеров на основе данных, исходя из максимизации среднего сходства между точками в кластере и минимизации между точками в разных кластерах.

Метод основан на формуле распространения удержания для привлечения кластеров к центральным точкам. Алгоритм начинается с выбора изначальных центральных точек, которые могут быть расположены на любых данных. Затем алгоритм итеративно распространяет и обновляет значения удержания и притяжения для каждой точки и каждого кластера.

Алгоритм прекращает работу, когда достигнута сходимость, и выводит определенное число кластеров с их центральными точками. Этот метод позволяет автоматически определить число групп без необходимости их предварительного задания и применяется для кластеризации различных типов данных, таких как изображения, текст, музыка, сетевые графы.

Средний сдвиг кластеризация

Средний сдвиг (англ. Average Shift) - это алгоритм кластеризации, который основан на понятии расстояния между точками в пространстве признаков. Методика исходит из того, что схожие объекты будут расположены близко друг к другу в пространстве признаков.

Алгоритм состоит из следующих шагов:

• инициализация начальных кластеров, например, каждая точка считается отдельным кластером;
• для каждой точки вычисляется среднее значение расстояния до всех остальных точек в некотором радиусе R;
• определяются новые центры кластеров с помощью точек, у которых среднее расстояние до других точек максимально;
• перевычисляется расстояние каждой точки до новых центров кластеров;
• если расстояние на данной итерации отличается от предыдущей меньше, чем заданный порог, то завершаем алгоритм.

Метод среднего сдвига обладает своими преимуществами и недостатками. Среди достоинств можно отметить хорошую адаптацию к форме и размеру кластеров. Не требуется указывать число кластеров заранее. Можно использовать центры кластеров в качестве их описания. Среди недостатков можно отметить остановку алгоритма, она зависит от выбранного порога. Локальный экстремум может привести к неверному результату. Неэффективность при больших объемах данных.

Спектральная кластеризация

Спектральная кластеризация - это метод машинного обучения, который использует матрицу смежности графа для разбиения множества элементов на кластеры. Он основан на идее, что элементы, находящиеся в одном кластере, имеют более сильные связи друг с другом, чем с элементами, принадлежащими к другим кластерам. В спектральной кластеризации матрица смежности графа преобразуется в матрицу Лапласа, которая затем подвергается спектральному разложению для получения собственных векторов. Они используются для проектирования элементов на новое пространство, где подвергаются кластеризации. Группирование является одним из самых популярных методов кластеризации, который широко используется в обработке изображений, биологии, маркетинге и других областях.

Различные стратегии присвоения меток в кластеризации

Существует несколько стратегий присвоения меток в кластеризации.

1. На основе ближайшего соседа (Nearest Neighbor Labeling): каждой точке в кластере присваивается метка большинства из меток ее ближайших соседей.
2. На основе центроида (Centroid Labeling): каждому кластеру присваивается метка, соответствующая самому типичному элементу этого кластера (центроиду).
3. На основе порогового значения (Threshold Labeling): задается пороговое значение, и все точки, которые находятся на расстоянии не большем, чем это значение, относятся к одному кластеру.
4. На основе иерархической кластеризации (Hierarchical Labeling): используются результаты иерархической кластеризации для присвоения меток.
5. На основе модели механизма генерации данных (Model Labeling): используется модель для описания данных и присвоения меток на основе вероятностей этой модели.

Иерархическая кластеризация — это метод группировки, который производит иерархическую декомпозицию данных на нарастающие уровни кластеров. Она относится к способам без учителя, что означает отсутствие заранее заданных классов или меток объектов. Иерархическая группировка может быть агломеративной (объединительной, начиная с отдельных точек) или дивизивной (разделяющей, начиная с одного кластера многих элементов). Во время обработки каждый элемент поначалу является отдельным кластером, постепенно объединяясь в более крупные кластеры на основе сходства между парами очередных объектов, а затем кластеры объединяются между собой, пока все объекты не будут объединены в один кластер. Результат иерархической группировки может быть представлен в виде дендрограммы, где расстояние между кластерами и является высотой соответствующей ветви дерева.